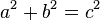Criptex;

 El passat dimecres els dos grups de criptografia formats el primer per Antonio, Irene, Laura L. i Xavi, i l' altre per Toni, Sandra i Lucia T. ens van explicar per separat l' historia de la criptografia i les seves aplicacions tant a l' antiguetat com a l' actualitat.

Grup Toni:

 Que es la criptografia? Dons la criptografia es la tecnica que altera les representacions linguistiques.
N' hi ha de dos tipus, la simetrica i la asimetrica.

 Simetrica: S' utilitza la mateixa clau per xifrar i per desxifrar. Per tant l' emissor i el receptor s' han de possar d' acord sobre quina clau van a utilitzar.
 Asimetrica: A aquesta tecnica s' utilitcen un parell de claus, una publica (que tothom coneix) i una privada (que nomes sap el propietari).

 Tambe es va parlar a aquesta exposicio sobre l' analisi de frequencies, que es l' estudi de la frequencia de les lletres a un text xifrat. Ens vam explicar alguns exemples com ara:

 Escitala: S' empraven dues bares del mateix grosor. I per enviar el missatge s' enrotllava una cinta en forma d' espiral a un dels bastons i s' escrivia el missatge de manera que a cada volta de cinta apareguera una lletra a cada volta. El receptor nomes tenia que enrotllar el missatge a la vara i es voria el missatge original.

 A,D,F,G,V,X: S' emprava una taula de 6x6 i es substituia qualsevol lletra del abecedari per una de les sis que ja he mencionat a la descripcio. Aquest metode tracta de buscar la concordancia de les dues lletres a la taula.

 Xifrat de Hill (xifratge simetric): Una de les seves caracteristiques es que es inmune a l' analisi de frequencies a diferencia d' altres sistemes monoalfabetics. Es mes rapid que un de clau publica. I la clau a de ser distribuida de forma confidencial. A l' hora de dexifrar el missatge es trobara que es distint al que s' ha enviat perque es trenca la frequencia del text original. Per ultim, la longitud dels dos missatges es la mateixa.
 A continuacio ens van explicar com es dexifraria un missatge per aquest metode.

 RSA (xifratge asimetric): l' RSA va solucionar el problema de tranferencia de la clau entre emissor i receptor. Es un metode modern que podem trobar p.e a les contrasenyes de wi-fi.
 A continuacio Toni va explicar com es dexifraria el missatge gracies a aquest metode.

Grup Antonio:

 A aquest grup es expliquen sobretot la part historica de la criptografia.

 La criptografia va sorgir practicament al mateix temps que l' escriptura. Els primers que van emprar aquest metode van ser els grecs i romans (com no), ja que era indispensable comunicar-se de manera secreta durant la guerra i els combats. Si el missatger que duia el missatge era capturat per l' enemic, aquest missatge no corria cap perill per que no mes podia dexifrar-lo el receptor.
 Diferents xifratges expicats pels companys:

 Xifratge Cesar:
 Rep el seu nom del Cesar, evidentment, que l' utilitzava per protegir els seus missatges militars. Es el xifratge mes emprat a la criptografia i consisteix en reassignar a cada lletra de l' abecedari un altra desplaçant les lletres un nombre concret, totes les lletres es desplaçaven el mateix nombre. En aquest cas Cesar emprava la clau 3. Es un xifratge simple monoalfabetic.

 Des de les mates: Es pot utilitzar aquest xifratge assignant a cada lletra un nombre.
 A continuacio s' explica el metode per desxifrar missatges dels nostres companys.

 Xifratge Vigenere:
 Es basa en diferents series de caracters o lletres del xifratge Cesar formant una taula, anomenada quadrat de Vigenere. A aquest quadrat a cada filera la posicio de les lletres es mou un nombre determinat de vegades i a la seguent filera un mes, i aixi succesivament.

 Per ultim es va explicar el xifratge Pig pen:
 A aquest xifratge es substituix cada lletra per un simbol. Es un xifratge monoalfabetic simple.
 A continuacio els companys de classe ens van explicar com es dexifren els missatges utilitzant aquesta tecnica.

Sinopsi de KIDS;

  A aquesta pel·licula s'observen els dos punts de vista del sexe que tenen dues xiques i dos xics. Aquesta pel·licula reflexa un dia a la vida d' aquestos quatre xics que nomes pensen en el sexe i en les drogues, un clar exemple de la societat neoyorquina de finals de segle XX. A consequencia d' aquesta vida i sorgixen problemes com ara que una de les dues xiques descobrix que te sida per haver praticat sexe sense precaucions aun que nomes hi haja practicat sexe amb una persona.

Fractals;

Hui a classe de mates han començat les exposicions dels treballs que han dut a terme els diferents grups durant tot el trimestre. Hui era el torn de Lucia, Laura i Mireia que han expossat el seu treball que tracta sobre els fractals.
Després d'aquesta exposició hem aprés algunes coses dels fractals:

Un fractal és una figura geométrica que té una estructura detallada a qualsevol escala i és autosemblant.
També ens han explicat com calcular una dimensió fractal, (provant amb la calculadora).
Després d' açò ens han donat exemples dels fractals, per dir-lo d' alguna
manera, més coneguts, com són:

El conjunt de Cantor:
Aquest fractal és autosemblant on l'última linea és semblant a la primera.
La construcció d'aquest fractal es senzilla:
Primer es divideix la primera linea en tres parts, i es lleva la del mig. I reiterant aquestos pasos es forma el conjunt de Cantor.

Altre exemple de fractal autosemblant és el de la Corba de Koch:

En aquest cas si agafes qualsevol part del fractal és semblant al primer.
La seva construcció es fa a partir d'un segment que es divit en tres segments, es lleva el segment del mig i al seu lloc es situa un triangle equilater i progressivament anirem fent açò.

El últim dels exemples es el del triangle de Sierpinski:
A aquest fractal autosemblant, cadascun dels triangles menuts és semblant al gran. Per a la seva construcció es necessari coneixer el punt mitjà dels triangles i s' unixen 3 triangles semblant al primer llevant el triangle del mig. Per un procés reiteratiu d' aquestes intruccions s' obté el triangle de Sierpinski.

Competencies;

Competencia 5:

Per a tindre aquesta competencia, has de ser conscient, gestionar i comprendre el control de les capacitats i coneixements, des d' un punt de vista competent i de superacio d' un mateix. Aquesta competencia inclou: el pensament estrategic, la capacitat de cooperar, la capacitat d' autoevaluar-se, maneig eficient de les tecniques que s' empren al treball intel·lectual. Tot aço es necessari per a tranformar-lo en coneixements propis de l' individu.

Des de les mates:

5. Aprendre a aprendre

Utilització de les eines matemàtiques en varietat de situacions.
Autonomia, perseverança i esforç per a abordar situacions de creixent complexitat, la sistematització, la mirada crítica i l'habilitat per a comunicar amb eficàcia els resultats del propi treball.
La verbalització del procés seguit en l'aprenentatge com a ajuda a la reflexió sobre què s'ha aprés, què falta per aprendre...

Puntuacio:

1.- Faig una recerca d' informacio, de la qual desconec la procedencia.
2.- Faig la recerca d' informacio, i conec la procedencia per aixi poder consultar-la en altre moment.
3.- Recerque l' informacio, conec la procedencia i se estructurar-la per escriure un text.
4.- Tinc l' informacio, tinc la font d' aquesta, se el·laborar un text per expossar-lo als meus companys i fer una bona presentacio.

Introducció sobre el treball de nombre phi;

Potser creieu que el nombre pi és el nombre irracional més important que hi podem trobar, per tindre relació amb la roda. Però hi algun nombre que es puga vore a la natura? I a l' arquitectura i pintura? Tal volta conegues algun que hi estiga més present a la geometria? Aquest és el nombre PHI. Des de les piràmides que construien el egipcis (a.C) fins la bresca d' abelles que podem trobar en una eixida al camp, el nombre phi, esta molt present a la nostra vida. Prepareu-vos per coneixer el nombre amb més aplicacions de la geometría, natura, arquitectura i pintura de tots els temps!

El meu prezi sobre phi a la natura;

PHI a la Natura on Prezi

KIDS;

Dema a atencio educativa continuarem veient la pel·licula KIDS, que tracta de la vida sexual de un grup de xics i xiques i de les seves distintes opinions i les formes de vore el sexe que tenen el dos generes.

Problema de les abelles de Fibonacci;

- Una abella mascle (borinot) prové d'un ou no fecundat, doncs té mare però no pare.
- Una abella femella prové d'un ou fecundat, doncs té mare i pare.
Estudia com evoluciona la quantitat d'avantpassats que tenen una abella mascle i una abella femella, i quina és la proporció (quocient) entre el nombre de femelles i el nombre de mascles d'una bresca.


M= abella mascle
F= abella femella

M
F
F M
F M F
F M F F M
F M F F M F M F
F M F F M F M F F M F F M

Aixi es compleix la succesio del matematic, pero tambe el podem vore una altra succesio des de que el primer individu es una femella:

F
F M
F M F
F M F F M
F M F F M F M F
F M F F M F M F F M F F M

Aquesta en compte de ser 1,1,3,5,8,13..., es 1,2,3,5,8,13...

Phi a les abelles;

Proporció metamorfològica de les abelles:

 La mesura de l'abdomen d'una abella dividit per phi és igual a la mesura del seu torax i a la mateixa mesura del torax dividida per phi és igual a la mesura de seu cap.

Phi a les plantes;

La disposició de les llavors d'un gira-sol està estructurada amb 21 espirals cap a l'esquerra i 34 cap a la dreta. Vint i trenta-quatre són dos nombres consecutius de la successió de Fibonacci: 1-1-2-3-5-8-13-21-34-55-89-144-233 ...

 El mateix ocorre amb les pinyes dels pins trobem dos nombres consecutius de la succesió de Fibonacci el 8 i el 13.

Phi al sistema solar;

Podem veure una relació amb phi a la distància dels diferents planetes del sistema solar al sol.

A la tercera columna de la següent taula el resultat es el de dividir la distància del planeta al sol per la distància anterior, per exemple la Terra dividim 

149.6 per 108.2 = 1.383.
 Per a Mercuri al no tindre un planeta anterior li hem assignat el nombre 1. 

Moltes vegades quan parlem del sistema solar ometem el cinturó d'asteroides, també representa una massa considerable en l '"equilibri del sistema solar", sent Ceres l'asteroide més gran. Ceres és tan gran que té una forma esfèrica (com els altres planetes) i representa un terç del total de la massa del cinturó d'asteroides situat entre Mart i Júpiter.

Planetas	Distancia al sol en millones de Km.	Relación entre las distancias de los sucesivos planetas
Mercurio	57,9	1
Venus	108,2	1,869
Tierra	149,6	1,383
Marte	227.9	1,523
Ceres	413,7	1,815
Júpiter	778,6	1,881
Saturno	1433,5	1,841
Urano	2872,5	2,004
Neptuno	4495,1	1,565
Plutón	5870	1,306

Total	16,187
Media	1,6187
Numero Phi	1,6180

Als anells de Cassini del planeta Saturn també es troba el nombre phi.

 Si el segment daurat es igual a 1, el segment blau es igual a phi.

Més phi a la natura;

Imatges del nombre phi a la natura:

On podem trobar el nombre auri al nostre voltant?
Al llarg de la història, des pensadors fins matemàtics o teòlegs han meditat sobre la misteriosa relació que s'estableix entre el nombre áureo i la naturalesa de la realitat. Aquesta curiosa relació matemàtica, coneguda popularment com la
Proporció Divina o Áurea, va ser definida per Euclides fa més de dos mil anys arran del seu paper crucial en la construcció del pentagrama, al qual se li atribueixen propietats màgiques.
Des de llavors, ha mostrat una propensió a aparèixer en una varietat de llocs d'allò més sorprenents que veurem a continuació:

 Girasol

El nombre auri també apareix en la formació dels flósculs dels gira-sols i en la disposició dels pètals d'algunes plantes com els cactus o roses:

 

Un altre exemple és el del cor de la POMA, a l'interior hi ha una curiosa estrella, anomenada estrella pentagonal

 

També regeix les dimensions i formes de GALÀXIES que contenen bilions d'estrelles i defineix la dinàmica dels forats negres. Però també podem trobar la bellesa de l'espiral de Dudero en HURACANS

Sinopsi Die Welle (La Ola)

Aquesta pel·lícula tracta del projecte de classe que fa un professor, tenen una semana per parlar d' autocracia, els alumnes es mostraven exceptics, ja que veien impossible que es formara una nova dictadura, perque tot el món estava concenciat amb el que va passar al tercer reich. Al llarg de la setmana els alumnes comencen a mostrar caracters típics d'una dictatura, com ara desplaçar a qui no vol formar part, vestir igual, una salutació entre ells, etc. Tots es senten units com a grup i no veuen el que estan fent. Finalment a la última sesió del projecte el mestre els mostra en que s' han convertit a causa d'aquest projecte i ells aprenen que si que podria haver tornat a passar una cosa tan horrible.

Fulles;

http://exapenta.zxq.net/HOJAS.html

A aquesta página trobarás fotografies de fulles que estan relacionades amb el nombre d' or.

Treball auri

TREBALL PHI (Mario, Alejandra, Jordi, Jorge)

Nombre phi a la natura:

A la natura, hi ha molts elements relacionats amb els Bonacci.

Bonacci, fa servir la succesió de nombres que porta el seu nom, per calcular el nombre de parells de conills després de que una pareja comence a reproduir-se.
El cocient de la succesió de Bonacci  es la secció àurea, si la fracció és propia o impropia.

La relació entre la quantitat d' abelles mascle i femelles a un panal.

La disposició dels pètals de les flors.

La distribució de les fulles en un tall.

La relació entre el grosor de les rames principals i el tronc, o entre les rames principals i les secundaries.

La distàcia entre les espirals d' una pinya.

La relació entre la distància de les espirals de l'interior de les espirals de cualsevol caragol.

Espirals como en el cas dels girasols, i altres objectes orgànics, es troben nombres de la succesió de Fibonacci. El cocient  de dos nombres d' aquesta succesió tendix al nombre auri.

Treball en grup;

 Després d' unes setmanes treballant amb el meu grup a classe de mates, hem decidit per fi en quin tema anem a aprofundir, anem a parlar del número phi



Mario buscarà informació sobre la relació entre el nombre phi i l'arquitectura.
Garrido buscarà sobre phi a la pintura.
Campos phi i geometria.
I jo parlaré de phi a la natura.

Les versions molen Lluís ;)

L' autoritat a Les Choristes;

  La pel·lícula ens mostra diferents técniques d' adoctrinament per als xiquets de l' internat.
Abans de l' arribada de Mathie el seu principi bàsic era acción, reacción, consistia en fer vore als xiquets que no podien anar-se de rosetes i que quan feien alguna de les seves debien pagar-ho severament, amb durs càstics, aïllament, maltracte físic, etc. L' arribada de Mathie suposa un canvi, els ensenya la manera de ser ells mateixos evitant fer canallades, i amb el cor els ajuda a fer una cosa que els agrade i de certa manera, canalitzar la seva rabia o frustració per tindre una infancia difícil.

 Als dos casos s' imposa que l' adult pot pissotejar al xiquet, però al mètode de Mathie podem veure que ell vol ser un líder respectat per ells i no odiat com succeix amb el director.

Sinopsi Les Choristes;

Aquesta pel·lícula tracta de l' estancia a un internat del vigilant Clément Mathie,que ens narrarà la seva experiència al centre i la seva técnica per donar una educació a xiquets conflictius a traves de la música i altres mètodes que els xiquets rebran de bona gana, en especial el jove i sigilós Pierre Morhange que descobrirà la seva passió per la música gràcies al cor del senyor Mathie.

El teorema de Pitàgores;

El teorema de Pitàgores en el seu enunciat habitual estableix que en un triangle rectangle la suma dels quadrats dels catets (els costats que formen l' angle recte) és igual al quadrat de la hipotenusa(l'altre costat).
El reciproc també es compleix, és a dir: en un triangle, si la suma dels quadrats de les longituds dels constats més curts és igual al quadrat de la longitud del costat més llarg, llavors l'angle comprès entre els dos costats més curts és un angle recte.
El teorema es pot escriure com una equació que relaciona les longituds dels costats a, b, i c, sovint anomenada l'equació de Pitàgores:

on c representa la longitud de la hipotenusa, i a i b representen les longituds dels altres dos costats.
El teorema de Pitàgores deu el nom al matemàtic grec Pitàgores, al que segons la tradició se li atribueix el seu descobriment i la demostració, encara que sovint s'argumenta que el coneixement del teorema era ja anterior. Hi ha proves que els matemàtics babilonis coneixien la fórmula, encara que ens ha arribat molt poca informació sobre l'ús que en feien.

              El teorema es refereix tant a les àrees com a les longituds, o pot dir-se que a les dues àrees i a les interpretacions mètriques. Algunes demostracions del teorema es basen en una interpretació, algunes sobre l'altre, utilitzant tècniques algebraiques i geomètriques. El teorema pot ser generalitzat de diverses maneres, incloent espais de dimensió superior, als espais no euclidians, als objectes que no són triangles rectangles i, de fet, als objectes que no són en tots els triangles, però són n-dimensionals sòlids. El teorema de Pitàgores ha despertat l'interès fora de les matemàtiques com un símbol de l' hermetisme de les matemàtiques, de la mística, o el poder intel·lectual; referències en la literatura popular, obre de teatre, abunden els musicals, cançons, segells i en els dibuixos animats.

Les Choristes

  Hui dijous hem acabat de vore la peli Los Chicos del coro, el próxim dia escriuré una redacció sobre un dels temes dels que tracta la peli. I l' expossarem el próxim dia a la classe d' atenció educativa.

 Una imatge del protagonista de la peli, Pierre Morhange.

Liber Abaci, Fibonacci.

Liber Abaci

Quan aparèixer el Liber Abaci de Leonardo per primera vegada, només uns pocs intel·lectuals europeus coneixien el números hindú-aràbics a través de traduccions dels escrits del matemàtic àrab del segle IX, Al-Khwarizmi.

En el Liber Abaci (1202) Fibonacci presenta l'anomenat modus Indorum (mètode dels indis), que avui es coneix com els nombres aràbics (Sigler 2003; Grimm 1973). El llibre propugna numeració amb els dígits 0-9 i en determina la seva notació proporcional. El llibre mostra la gran practicitat d'aquest "nou" sistema de numeració, mitjançant l'ús de la multiplicació per gelosia (tipus de multiplicació algorítmica) i la fracció egipciana, tot aplicant-lo a la comptabilitat, la conversió de mesures i pesos, càlculs d'interès, canvi de monedes i altres aplicacions.
El llibre fou molt ben rebut a tot Europa instruïda tot provocant un profund impacte en el pensament europeu.
Liber Abaci també planteja, i resol, un problema que implica el creixement d'una hipotètica població de conills sobre una base de supòsits idealitzada. La solució, generació per generació, és una seqüència de nombres més tard coneguda com succesió de Fibonacci. Dita seqüència, no obstant, ja era coneguda per matemàtics indis en el segle VI,  però fou Fibonacci, mitjançant aquest llibre, qui la va introduir a Occident.

Fibonacci;

Leonardo de Pisa (c. 1170 – c. 1250), també conegut com a Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, o, de forma més comuna, simplement Fibonacci, fou un matemàtic italià, potser un dels matemàtics amb més talent de l'edat mitjana. Féu nombrosos viatges per tota l'àrea de la Mediterrània: Síria, Egipte, Grècia, França, Sicília i el nord d'Àfrica.
Fibonacci és conegut actualment per:

• Haver contribuït a la difusió del sistema de numeració hindú-aràbic a Europa, sobretot degut a la publicació a principis del segle XIII del seu Llibre dels càlculs, el Liber Abaci.
• Una succesió numèrica molt utilitzada, coneguda amb el seu nom com a succesió de Fibonacci, que va utilitzar com a exemple en el Liber Abaci.

Aplicà l'algebra als problemes geomètrics. Desenvolupà la trigonometria i féu treballs interessants sobre les equacions quadràtiques

 
El conegut problema de les llebres de Fibonacci, ilustrat al dimoni dels nombres que vam llegir aquest estiu.

Monedes italianes de 1 i 2 euros.

    Moneda de 2€ on ix la cara de Dante, un conegut poeta Italià nascut a Florència i moneda d' 1€ on ix el conegut dibuix de l' inventor Leonardo da Vinci l' home de Vitruvi.

Dimarts 13, dia de la mala sort.

           A les cultures de Espanya, Grècia i Llatinoamerica el dimarts 13 es considerat per exelencia el dia de la mala sort. Existeix un refran espanyol que diu: En martes 13 ni te cases ni te embarques. Açò ens diu que si contraiem matrimoni o eixim de viatge aquest dia les coses no aniram massa bé.
          Molta gent li te fobia aquest dia i preferix no anar a cap lloc si es aquesta la dada senyalada, aquesta fobia es coneguda com la Trezidavomartiofobia. També és una curiositat que els avions no tinguen fila número 13 perque no es comprarien billets per aquesta filera.

          Aquesta superstició no te cap base científica, i es supossat que es tracta de un mite. Inclós hi ha gent que hi creu que el dimarts 13 és dia de bona sort i decideixen gastar diners en jocs d' azar.

         A les cultures anglosaxones el dia de la mala sort es el divendres 13 y a la cultura italiana hi és el divendres 17. Però a totes les cultures té les mateixes connotacions.


       -Per què 13?

        Per que desde l' antiguitat el 13 es conegut com un nombre de mala sort. Algunes dades que es citen son l' últim sopar de Jesucrist, on eren 12 apostols més ell, i es considera a Judas el traidor com número 13. A la Cábala s'enumeren 13 esperits malignes, al igual que les llegendes nórdiques; al Apocalipsis el capítol número 13 fa referencia a la bestia i l' anticrist. I a més, al tarot, aquest nombre fa referéncia a la mort.

        -Per què el dimarts?
       
         L' aportació de que siga dimarts el dia, va sorgir a final de l' Edat Mitjana, ja que el dimarts 29 de maig de 1453 va caure la ciutat de Constantinoble. La caiguda de Constantinoble va suposar un enorme trauma per a les potències cristianes, i el dia de la seva caiguda, dimarts, associat a un déu pagà va ser considerat des de llavors, dia de la mala sort.