El reciproc també es compleix, és a dir: en un triangle, si la suma dels quadrats de les longituds dels constats més curts és igual al quadrat de la longitud del costat més llarg, llavors l'angle comprès entre els dos costats més curts és un angle recte.
El teorema es pot escriure com una equació que relaciona les longituds dels costats a, b, i c, sovint anomenada l'equació de Pitàgores:
El teorema de Pitàgores deu el nom al matemàtic grec Pitàgores, al que segons la tradició se li atribueix el seu descobriment i la demostració, encara que sovint s'argumenta que el coneixement del teorema era ja anterior. Hi ha proves que els matemàtics babilonis coneixien la fórmula, encara que ens ha arribat molt poca informació sobre l'ús que en feien.
El teorema es refereix tant a les àrees com a les longituds, o pot dir-se que a les dues àrees i a les interpretacions mètriques. Algunes demostracions del teorema es basen en una interpretació, algunes sobre l'altre, utilitzant tècniques algebraiques i geomètriques. El teorema pot ser generalitzat de diverses maneres, incloent espais de dimensió superior, als espais no euclidians, als objectes que no són triangles rectangles i, de fet, als objectes que no són en tots els triangles, però són n-dimensionals sòlids. El teorema de Pitàgores ha despertat l'interès fora de les matemàtiques com un símbol de l' hermetisme de les matemàtiques, de la mística, o el poder intel·lectual; referències en la literatura popular, obre de teatre, abunden els musicals, cançons, segells i en els dibuixos animats.
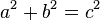


No hay comentarios:
Publicar un comentario